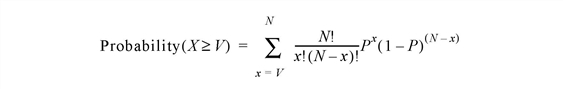
The BINOMIAL function computes the probability that in a cumulative binomial (Bernoulli) distribution, a random variable X is greater than or equal to a user-specified value V, given N independent performances and a probability of occurrence or success P in a single performance:
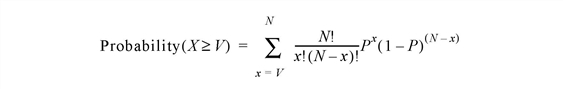
This routine is written in the IDL language. Its source code can be found in the file binomial.pro in the lib subdirectory of the IDL distribution.
Result = BINOMIAL(V, N, P [, /DOUBLE] [, /GAUSSIAN] )
This function returns a single- or double-precision floating point scalar or array that contains the value of the probability.
A non-negative integer specifying the minimum number of times the event occurs in N independent performances.
A non-negative integer specifying the number of performances.
A non-negative single- or double-precision floating-point scalar or array, in the interval [0.0, 1.0], that specifies the probability of occurrence or success of a single independent performance.
Set this keyword to force the computation to be done in double-precision arithmetic.
Set this keyword to use the Gaussian approximation, by using the normalized variable Z = (V – NP)/SQRT(NP(1 – P)).
Note: The Gaussian approximation is useful when N is large and neither P nor (1–P) is close to zero, where the binomial summation may overflow. If GAUSSIAN is not explicitly set, and the binomial summation overflows, then BINOMIAL will automatically switch to using the Gaussian approximation.
Compute the probability of obtaining at least two 6s in rolling a die four times. The result should be 0.131944.
result = BINOMIAL(2, 4, 1.0/6.0)
print, result
Compute the probability of obtaining exactly two 6s in rolling a die four times. The result should be 0.115741.
result = BINOMIAL(2, 4, 1./6.) - BINOMIAL(3, 4, 1./6.)
print, result
Compute the probability of obtaining three or fewer 6s in rolling a die four times. The result should be 0.999228.
result = BINOMIAL(0, 4, 1./6.) - BINOMIAL(4, 4, 1./6.)
print, result
|
Pre 4.0 |
Introduced |
CHISQR_PDF , F_PDF , GAUSS_PDF , T_PDF