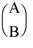Open topic with navigation

LA_LEAST_SQUARE_EQUALITY

Syntax | Return Value | Arguments | Keywords | Examples | Version History | See Also

The LA_LEAST_SQUARE_EQUALITY function is used to solve the linear least-squares problem:

Minimize_x ||Ax - c||₂ with constraint Bx = d

where A is an n-column by m-row array, B is an n-column by p-row array, c is an m-element input vector, and d is an p-element input vector with p ≤ n ≤ m+p. If B has

full row rank p and the array 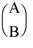has full column rank n, then a unique solution exists.

LA_ LEAST_SQUARE_EQUALITY is based on the following LAPACK routines:

For details see Anderson et al., LAPACK Users' Guide, 3rd ed., SIAM, 1999.

Syntax

Result = LA_LEAST_SQUARE_EQUALITY( A, B, C, D [, /DOUBLE] [, RESIDUAL=variable] )

Return Value

The result (x) is an n-element vector.

Arguments

A

The n-by-m array used in the least-squares minimization.

B

The n-by-p array used in the equality constraint.

C

An m-element input vector containing the right-hand side of the least-squares system.

D

A p-element input vector containing the right-hand side of the equality constraint.

Keywords

DOUBLE

Set this keyword to use double-precision for computations and to return a double-precision (real or complex) result. Set DOUBLE = 0 to use single-precision for computations and to return a single-precision (real or complex) result. The default is /DOUBLE if A is double precision, otherwise the default is DOUBLE = 0.

RESIDUAL

Set this keyword to a named variable in which to return a scalar giving the residual sum-of-squares for Result. If n = m + p then RESIDUAL will be zero.

Examples

Given the following system of equations:

2t + 5u + 3v + 4w = 9

7t + u + 3v + 5w = 1

4t + 3u + 6v + 2w = 2

with constraints,

-3t + u + 2v + 4w = -4

2t + 5u + 9v + 1w = 4

find the solution using the following code:

; Define the coefficient array:
a = [[2, 5, 3, 4], $
   [7, 1, 3, 5], $
   [4, 3, 6, 2]]

; Define the constraint array:
b = [[-3, 1, 2, 4], $
   [2, 5, 9, 1]]

; Define the right-hand side vector c:
c = [9, 1, 2]

; Define the constraint right-hand side d:
d = [-4, 4]

; Find and print the minimum norm solution of a:
x = LA_LEAST_SQUARE_EQUALITY(a, b, c, d)
PRINT, 'LA_LEAST_SQUARE_EQUALITY solution:'
PRINT, x

IDL prints:

LA_LEAST_SQUARE_EQUALITY solution:

0.651349 2.72695 -1.14638 -0.620036

Version History

See Also

LA_GM_LINEAR_MODEL , LA_LEAST_SQUARES