The RANDOMN function returns one or more pseudo-random numbers with one of the following distributions: Gaussian (the default), binomial, gamma, Poisson, or uniform.
RANDOMN uses the Box-Muller method for generating normally-distributed (Gaussian) random numbers. The algorithm is based off of the gasdev algorithm given in Section 7.2 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press. The formulas for the binomial, gamma, and Poisson distributions are from section 7.3 of Numerical Recipes in C. For more discussion of the random number generation in IDL, see the RANDOMU function.
Result = RANDOMN( Seed[, D1[, ..., D8]] [ [, BINOMIAL=[trials, probability]] [, /DOUBLE] [, GAMMA=integer{>0}] [, /NORMAL] [, POISSON=value] [, /UNIFORM] | [, /LONG] ] )
Returns an array containing the random numbers of the specified dimensions.
A variable or constant used to initialize the random sequence on input, and in which the state of the random number generator is saved on output. See the description of the Seed argument in the RANDOMU function for details.
Either an array or a series of scalar expressions specifying the dimensions of the result. If a single argument is specified, it can be either a scalar expression or an array of up to eight elements. If multiple arguments are specified, they must all be scalar expressions. Up to eight dimensions can be specified. If no dimensions are specified, RANDOMN returns a scalar result
Set this keyword to a 2-element array, [n, p], to generate random deviates from a binomial distribution. If an event occurs with probability p, with n trials, then the number of times it occurs has a binomial distribution.
Note: For n > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to force the computation to be done using double-precision arithmetic.
RANDOMN constructs double-precision uniform random deviates using the formula:
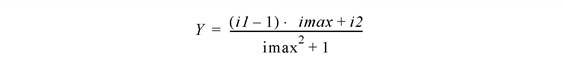
where i1 and i2 are integer random deviates in the range [1...imax], and imax = 231 - 2 is the largest possible integer random deviate. The Y values will be in the range 0 < Y < 1.
Set this keyword to an integer order i > 0 to generate random deviates from a gamma distribution. The gamma distribution is the waiting time to the ith event in a Poisson random process of unit mean. A gamma distribution of order equal to 1 is the same as the exponential distribution.
Note: For GAMMA > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to return integer uniform random deviates in the range [1...231 – 2]. If LONG is set, all other keywords are ignored.
Set this keyword to generate random deviates from a normal distribution with a mean of zero and a standard deviation of 1. This is the default.
Set this keyword to the mean number of events occurring during a unit of time. The POISSON keyword returns a random deviate drawn from a Poisson distribution with that mean.
Note: For POISSON > 1.0 x 107, you should set the DOUBLE keyword.
Set this keyword to generate random deviates from a uniform distribution. Using this keyword is equivalent to calling the RANDOMU function.
If you start the sequence with an undefined variable—if RANDOMN has already been called, Seed is no longer undefined—IDL initializes the sequence with the system time:
; Generate one random variable and initialize the sequence with an
; undefined variable:
randomValue = RANDOMN(seed)
The new state is saved in seed. To generate repeatable experiments, begin the sequence with a particular seed:
seed_value = 5L
; Generate one random variable and initialize the sequence with 5:
randomValue = RANDOMN(seed_value)
PRINT, randomValue
IDL prints:
0.521414
To restart the sequence with a particular seed, re-initialize the variable:
seed = 5L
;Get a normal random number, and restart the sequence with a seed
;of 5.
randomValue = RANDOMN(seed)
PRINT, randomValue
IDL prints:
0.521414
To continue the same sequence:
PRINT, RANDOMN(seed)
IDL prints:
-0.945489
To create a 10 by 10 array of normally-distributed, random numbers, type:
R = RANDOMN(seed, 10, 10)
Since seed is undefined, the generic state is used to initialize the random number generator. Print the resulting values by entering:
PRINT, R
A more interesting example plots the probability function of 2000 numbers returned by RANDOMN. Type:
PLOT, HISTOGRAM(RANDOMN(SEED, 2000), BINSIZE=0.1)
To obtain a sequence of 1000 exponential (gamma distribution, order 1) deviates, type:
Result = RANDOMN(seed, 1000, GAMMA=1)
Intuitively, the result contains a random series of waiting times for events occurring an average of one per time period.
To obtain a series of 1000 random elapsed times required for the arrival of two events, type:
;Returns a series of 1000 random elapsed times required for the
;arrival of two events.
Result = RANDOMN(seed, 1000, GAMMA=2)
To obtain a 128 x 128 array filled with Poisson deviates, with a mean of 1.5, type:
Result = RANDOMN(seed, 128, 128, POISSON=1.5)
To simulate the count of “heads” obtained when flipping a coin 10 times, type:
Result = RANDOMN(seed, BINOMIAL=[10,.5])
|
Original |
Introduced |