DFTI_COMPLEX_STORAGE, DFTI_REAL_STORAGE, DFTI_CONJUGATE_EVEN_STORAGE

Depending on the value of configuration parameter DFTI_FORWARD_DOMAIN, the implementation of FFT supports several storage schemes for input and output data (see document [3] for the rationale behind the definition of the storage schemes). The data elements are placed within contiguous memory blocks, defined with generalized strides (see DFTI_INPUT_STRIDES, DFTI_OUTPUT_STRIDES). For multiple transforms an nth set of data (nth begins with zero) should be located within the same memory block, and the data sets are placed at a distance from each other (see DFTI_NUMBER_OF TRANSFORMS and DFTI_INPUT DISTANCE, DFTI_OUTPUT_DISTANCE).

Note

In C/C++, avoid setting up multidimensional arrays with lists of pointers to one-dimensional arrays. Instead use a one-dimensional array with the explicit indexing to access the data elements.

The C/C++ notation is used to precisely describe association of mathematical entities with the data elements stored in memory. FFT Examples demonstrate the usage of storage formats in C and Fortran.

Storage schemes for complex domain. For the DFTI_COMPLEX forward domain, both input and output sequences belong to the complex domain. In this case, configuration parameter DFTI_COMPLEX_STORAGE can have one of the two values: DFTI_COMPLEX_COMPLEX (default) or DFTI_REAL_REAL.

Note

In the Intel MKL FFT implementation, storage schemes for a forward complex domain and the respective backward complex domain are the same.

With DFTI_COMPLEX_COMPLEX storage, the complex-valued data sequence is referenced by a single data parameter Z associated with the complex type so that complex-valued element z_{k1, k2, ..., kd} of the sequence is located at Z[nth*distance + stride₀ + k₁*stride₁ + k₂*stride₂+ ... k_d*stride_d] as a structure consisting of the real and imaginary parts.

The following example illustrates a typical usage of the DFTI_COMPLEX_COMPLEX storage:

complex :: x(n)

...

! on input, for i=1,...,N: x(i) = wi-1

status = DftiComputeForward( desc_handle, x )

! on output, for i=1,...,N: x(i) = zi-1

With the DFTI_REAL_REAL storage, the complex-valued data sequence is referenced by two data parameters ZRe and ZIm , both associated with the real type so that complex-valued element z_{k1, k2, ..., kd} of the sequence is computed as ZRe[nth*distance + stride₀ + k₁*stride₁ + k₂*stride₂+ ... k_d*stride_d] + √(-1) × ZIm[nth*distance + stride₀ + k₁*stride₁ + k₂*stride₂+ ... k_d*stride_d].

A typical usage of the DFTI_REAL_REAL storage is illustrated by the following example:

real :: xre(n), xim(n)

...

status = DftiSetValue( desc_handle, DFTI_COMPLEX_STORAGE, DFTI_REAL_REAL)

! on input, for i=1,...,N: cmplx(xre(i),xim(i)) = wi-1

status = DftiComputeForward( desc_handle, xre, xim )

! on output, for i=1,...,N: cmplx(xre(i),xim(i)) = zi-1

Storage scheme for the real and conjugate-even domains. This setting for the storage schemes for these domains is recorded in the configuration parameters DFTI_REAL_STORAGE and DFTI_CONJUGATE_EVEN_STORAGE. Since a forward real domain corresponds to a conjugate-even backward domain, they are considered together. The example uses one-, two- and three-dimensional real to conjugate-even transforms. In-place computation is assumed whenever possible (that is, when the input data type matches the output data type).

One-Dimensional Transform

Consider a one-dimensional n-length transform of the form

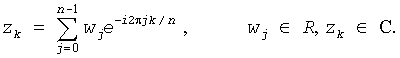
There is a symmetry:

For even n: z(n/2+i) = conjg(z(n/2-i)), 1≤i≤n/2-1, and moreover z(0) and z(n/2) are real values.

For odd n: z(m+i) = conjg(z(m-i+1)), 1≤i≤m, and moreover z(0) is real value.

m = floor(n/2).

Assume that the stride has the default value (unit stride).

This complex conjugate-symmetric vector can be stored in the complex array of size m+1 or in the real array of size 2m+2 or 2m depending on packed format.

Two-Dimensional Transform

Each of the real-to-complex functions computes the forward FFT of a two-dimensional real matrix according to the mathematical equation

t_k,l = cmplx(r_k,l,0), where r_k,l is a real input matrix, 0≤k≤m-1, 0 ≤l≤n-1. The mathematical result z_i,j, 0≤i≤m-1, 0≤j≤n-1, is the complex matrix of size (m,n). Each column is the complex conjugate-symmetric vector as follows:

For even m:

for 0 ≤j≤n-1,

z(m/2+i,j) = conjg(z(m/2-i,j)),1≤i≤m/2-1.

Moreover, z(0,j) and z(m/2,j) are real values for j=0 and j=n/2.

For odd m:

for 0≤j≤n-1,

z(s+i,j) = conjg(z(s-i,j)), 1≤i≤s-1,

where s = floor(m/2).

Moreover, z(0,j) are real values for j=0 and j=n/2.

This mathematical result can be stored in the real two-dimensional array of size:

or in the complex two-dimensional array of size:

Since the multidimensional array data are arranged differently in Fortran and C (see DFTI_INPUT_STRIDES, DFTI_OUTPUT_STRIDES), the output array that holds the computational result contains complex conjugate-symmetric columns (for Fortran) or complex conjugate-symmetric rows (for C).

The following tables give examples of output data layout in Pack format for a forward two-dimensional real-to-complex FFT of a 6-by-4 real matrix. Note that the same layout is used for the input data of the corresponding backward complex-to-real FFT.

For the above example, the stride array is taken to be (0, 1, 6).

For the second example, the stride array is taken to be (0, 4, 1).

See also DFTI_PACKED_FORMAT.

Three-Dimensional Transform

Each of the real-to-complex functions computes the forward FFT of a three-dimensional real matrix according to the mathematical equation

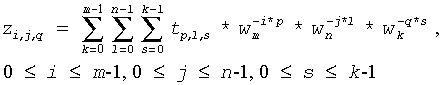
t_p,l,s = cmplx(r_p,l,s,0), where r_p,l,s is a real input matrix, 0 ≤ k ≤ m-1, 0 ≤ l ≤ n-1, 0 ≤ s ≤ k-1. The mathematical result z_i,j,q, 0 ≤ i ≤ m-1, 0 ≤ j ≤ n-1, 0 ≤ q ≤ k-1 is the complex matrix of size (m,n,k), which is a complex conjugate-symmetric, or conjugate-even, matrix as follows:

z_m1,n1,k1 = conjg(z_{m-m1,n-n1,k-k1}), where each dimension is periodic.

This mathematical result can be stored in the real three-dimensional array of size:

Since the multidimensional array data are arranged differently in Fortran and C (see DFTI_INPUT_STRIDES, DFTI_OUTPUT_STRIDES), the output array that holds the computational result contains complex conjugate-symmetric columns (for Fortran) or complex conjugate-symmetric rows (for C).

Note

There is one packed format for 3D REAL FFT - CCE format. In both in-place and out-of-place REAL FFT, for real data, the stride and distance parameters are in REAL units and for complex data, they are in COMPLEX units. So, elements of input and output data can be placed in different elements of input-output array of the in-place FFT.

1. DFTI_REAL_REAL for real domain, DFTI_COMPLEX_REAL for conjugate-even domain (by default). It is used for 1D and 2D REAL FFT.

   • A typical usage of in-place transform is as follows:

     // m = floor( n/2 )

     REAL :: X(0:2*m+1)

     ...some other code...

     ...assuming inplace transform...

     Status = DftiComputeForward( Desc_Handle, X )

     On input,

     X(j) = w_j, j = 0,1,...,n-1.

     On output,

     Output data stored in one of formats: Pack, Perm or CCS (see DFTI_PACKED_FORMAT).

     CCS format: X(2*k) = Re(z_k), X(2*k+1) = Im(z_k), k = 0,1,...,m.

     Pack format:

     even n: X(0) = Re(z₀), X(2*k-1) = Re(z_k), X(2*k) = Im(z_k), k = 1,...,m-1, and X(n-1) = Re(z_m)

     odd n: X(0) = Re(z₀), X(2*k-1) = Re(z_k), X(2*k) = Im(z_k), k = 1,...,m

     Perm format:

     even n: X(0) = Re(z₀), X(1) = Re(z_m), X(2*k) = Re(z_k), X(2*k+1) = Im(z_k), k = 1,...,m-1,

     odd n: X(0) = Re(z₀), X(2*k-1) = Re(z_k), X(2*k) = Im(z_k), k = 1,...,m.

     See Example "One-dimensional In-place FFT (Fortran Interface)", Example "One-dimensional In-place FFT (C Interface)", Example "Two-dimensional FFT (Fortran Interface)", and Example "Two-dimensional FFT (C Interface)".

     Input and output data exchange the roles in the backward transform.

   • A typical usage of out-of-place transform is as follows:

     // m = floor( n/2 )

     REAL :: X(0:n-1)

     REAL :: Y(0:2*m+1)

     ...some other code...

     ...assuming out-of-place transform...

     Status = DftiComputeForward( Desc_Handle, X, Y )

     On input, X(j) = w_j, j = 0,1,...,n-1.

     On output,

     Output data stored in one of formats: Pack, Perm or CCS (see DFTI_PACKED_FORMAT).

     CCS format: Y(2*k) = Re(z_k), Y(2*k+1) = Im(z_k), k = 0,1,...,m.

     Pack format:

     even n: Y(0) = Re(z₀), Y(2*k-1) = Re(z_k), Y(2*k) = Im(z_k), k = 1,...,m-1, and Y(n-1) = Re(z_m)

     odd n: Y(0) = Re(z₀), Y(2*k-1) = Re(z_k), Y(2*k) = Im(z_k), k = 1,...,m

     Perm format:

     even n: Y(0) = Re(z₀), Y(1) = Re(z_m), Y(2*k) = Re(z_k) , Y(2*k+1) = Im(z_k), k = 1,...,m-1,

     odd n: Y(0) = Re(z₀), Y(2*k-1) = Re(z_k), Y(2*k) = Im(z_k), k = 1,...,m.

     Notice that if the stride of the output array is not set to the default value unit stride, the real and imaginary parts of one complex element will be placed with this stride.

     For example:

     CCS format: Y(2*k*s) = Re(z_k), Y((2*k+1)*s) = Im(z_k), k = 0,1, ..., m, s - stride.

     See Example "One-dimensional Out-of-place FFT (Fortran Interface)" and Example "One-dimensional Out-of-place FFT (C Interface)".

     Input and output data exchange the roles in the backward transform.

2. DFTI_REAL_REAL for real domain, DFTI_COMPLEX_COMPLEX for conjugate-even domain. It is used for 1D, 2D and 3D REAL FFT. The CCE format is set by default. You must explicitly set the storage scheme in this case, because its value is not the default one.

   • A typical usage of in-place transform is as follows:

     // m = floor( n/2 )

     REAL :: X(0:m*2)

     ...some other code...

     ...assuming in-place transform...

     Status = DftiSetValue( Desc_Handle,  DFTI_CONJUGATE_EVEN_STORAGE, DFTI_COMPLEX_COMPLEX)

     ...

     Status = DftiComputeForward( Desc_Handle, X)

     On input,

     X(j) = w_j, j = 0,1,...,n-1.

     On output,

     X(2*k) = Re(z_k), X(2*k+1) = Im(z_k), k = 0,1,...,m.

     See Example "Two-Dimensional REAL In-place FFT (Fortran Interface)".

     Input and output data exchange the roles in the backward transform.

   • A typical usage of out-of-place transform is as follows:

     // m = floor( n/2 )

     REAL :: X(0:n-1)

     COMPLEX :: Y(0:m)

     ...some other code...

     ...assuming out-of-place transform...

     Status = DftiSetValue( Desc_Handle,  DFTI_CONJUGATE_EVEN_STORAGE, DFTI_COMPLEX_COMPLEX)

     ...

     Status = DftiComputeForward( Desc_Handle, X, Y )

     On input,

     X(j) = w_j, j = 0,1,...,n-1.

     On output,

     Y(k) = z_k, k = 0,1,...,m.

     See Example "Two-Dimensional REAL Out-of-place FFT (Fortran Interface)" and Example "Three-Dimensional REAL FFT (C Interface)"

     Input and output data exchange the roles in the backward transform.

3. DFTI_REAL_COMPLEX for real domain, DFTI_COMPLEX_COMPLEX for conjugate-even domain. It is not used in the current version. See the Note for details. A typical usage is as follows:

   // m = floor( n/2 )

   COMPLEX :: X(0:m)

   ...some other code...

   ...inplace transform...

   Status = DftiComputeForward( Desc_Handle, X )

   On input,

   X(j) = w_j, j = 0,1,...,n-1.

   That is, the imaginary parts of X(j) are zero.

   On output,

   Y(k) = z_k, k = 0,1,...,m,

   where m is floor( n/2 ).