?gglse

Syntax

FORTRAN 77:

call sgglse(m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)

call dgglse(m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)

call cgglse(m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)

call zgglse(m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)

Fortran 95:

call gglse(a, b, c, d, x [,info])

C:

lapack_int LAPACKE_<?>gglse( int matrix_order, lapack_int m, lapack_int n, lapack_int p, <datatype>* a, lapack_int lda, <datatype>* b, lapack_int ldb, <datatype>* c, <datatype>* d, <datatype>* x );

Include Files

The FORTRAN 77 interfaces are specified in the mkl_lapack.fi and mkl_lapack.h include files, the Fortran 95 interfaces are specified in the lapack.f90 include file, and the C interfaces are specified in the mkl_lapacke.h include file.

Description

The routine solves the linear equality-constrained least squares (LSE) problem:

minimize ||c - A*x||² subject to B*x = d

where A is an m-by-n matrix, B is a p-by-n matrix, c is a given d is a given p-vector. It is assumed that p ≤ n ≤ m+p, and

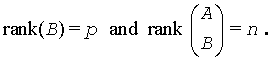
These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by

B=(0 R)*Q, A=Z*T*Q

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

m

INTEGER. The number of rows of the matrix A (m ≥ 0).

n

INTEGER. The number of columns of the matrices A and B (n ≥ 0).

p

INTEGER. The number of rows of the matrix B

(0 ≤ p ≤ n ≤ m+p).

a, b, c, d, work

REAL for sgglse

DOUBLE PRECISION for dgglse

COMPLEX for cgglse

DOUBLE COMPLEX for zgglse.

Arrays:

a(lda,*) contains the m-by-n matrix A.

The second dimension of a must be at least max(1, n).

b(ldb,*) contains the p-by-n matrix B.

The second dimension of b must be at least max(1, n).

c(*), dimension at least max(1, m), contains the right hand side vector for the least squares part of the LSE problem.

d(*), dimension at least max(1, p), contains the right hand side vector for the constrained equation.

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, m).

ldb

INTEGER. The leading dimension of b; at least max(1, p).

lwork

INTEGER. The size of the work array;

lwork ≥ max(1, m+n+p).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

See Application Notes for the suggested value of lwork.

Output Parameters

x

REAL for sgglse

b

On exit, the upper triangle of the subarray b(1:p, n-p+1:n) contains the p-by-p upper triangular matrix R.

d

On exit, d is destroyed.

c

On exit, the residual sum-of-squares for the solution is given by the sum of squares of elements n-p+1 to m of vector c.

work(1)

If info = 0, on exit, work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the upper triangular factor R associated with B in the generalized RQ factorization of the pair (B, A) is singular, so that rank(B) < P; the least squares solution could not be computed.

If info = 2, the (n-p)-by-(n-p) part of the upper trapezoidal factor T associated with A in the generalized RQ factorization of the pair (B, A) is singular, so that

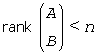
; the least squares solution could not be computed.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see Fortran 95 Interface Conventions.

Specific details for the routine gglse interface are the following:

a

Holds the matrix A of size (m,n).

b

Holds the matrix B of size (p,n).

c

Holds the vector of length (m).

d

Holds the vector of length (p).

x

Holds the vector of length n.

Application Notes

For optimum performance, use

lwork ≥ p + min(m, n) + max(m, n)*nb,

where nb is an upper bound for the optimal blocksizes for ?geqrf, ?gerqf, ?ormqr/?unmqr and ?ormrq/?unmrq.

You may set lwork to -1. The routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if you set lwork to less than the minimal required value and not -1, the routine returns immediately with an error exit and does not provide any information on the recommended workspace.