?orbdb/?unbdb

Syntax

FORTRAN 77:

call sorbdb( trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, phi, taup1, taup2, tauq1, tauq2, work, lwork, info )

call dorbdb( trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, phi, taup1, taup2, tauq1, tauq2, work, lwork, info )

call cunbdb( trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, phi, taup1, taup2, tauq1, tauq2, work, lwork, info )

call zunbdb( trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, phi, taup1, taup2, tauq1, tauq2, work, lwork, info )

Fortran 95:

call orbdb( x11,x12,x21,x22,theta,phi,taup1,taup2,tauq1,tauq2[,trans][,signs][,info] )

call unbdb( x11,x12,x21,x22,theta,phi,taup1,taup2,tauq1,tauq2[,trans][,signs][,info] )

C:

lapack_int LAPACKE_sorbdb( int matrix_order, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, float* x11, lapack_int ldx11, float* x12, lapack_int ldx12, float* x21, lapack_int ldx21, float* x22, lapack_int ldx22, float* theta, float* phi, float* taup1, float* taup2, float* tauq1, float* tauq2 );

lapack_int LAPACKE_dorbdb( int matrix_order, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, double* x11, lapack_int ldx11, double* x12, lapack_int ldx12, double* x21, lapack_int ldx21, double* x22, lapack_int ldx22, double* theta, double* phi, double* taup1, double* taup2, double* tauq1, double* tauq );

lapack_int LAPACKE_cunbdb( int matrix_order, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, lapack_complex_float* x11, lapack_int ldx11, lapack_complex_float* x12, lapack_int ldx12, lapack_complex_float* x21, lapack_int ldx21, lapack_complex_float* x22, lapack_int ldx22, float* theta, float* phi, lapack_complex_float* taup1, lapack_complex_float* taup2, lapack_complex_float* tauq1, lapack_complex_float* tauq2 );

lapack_int LAPACKE_zunbdb( int matrix_order, char trans, char signs, lapack_int m, lapack_int p, lapack_int q, lapack_complex_double* x11, lapack_int ldx11, lapack_complex_double* x12, lapack_int ldx12, lapack_complex_double* x21, lapack_int ldx21, lapack_complex_double* x22, lapack_int ldx22, double* theta, double* phi, lapack_complex_double* taup1, lapack_complex_double* taup2, lapack_complex_double* tauq1, lapack_complex_double* tauq2 );

Include Files

The FORTRAN 77 interfaces are specified in the mkl_lapack.fi and mkl_lapack.h include files, the Fortran 95 interfaces are specified in the lapack.f90 include file, and the C interfaces are specified in the mkl_lapacke.h include file.

Description

The routines ?orbdb/?unbdb simultaneously bidiagonalizes the blocks of an m-by-m partitioned orthogonal matrix X:

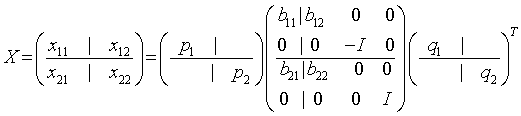
or unitary matrix:

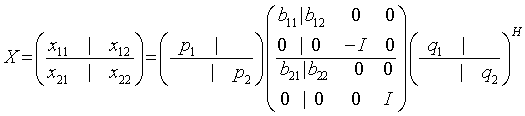
x₁₁ is p-by-q. q must not be larger than p, m-p, or m-q. Otherwise, x must be transposed and/or permuted in constant time using the trans and signs options. See ?orcsd/?uncsd for details.

The orthogonal/unitary matrices p₁, p₂, q₁, and q ₂ are p-by-p, (m-p)-by-(m-p), q-by-q, (m-q)-by-(m-q), respectively. They are represented implicitly by Housholder vectors.

The bidiagonal matrices b₁₁, b₁₂, b₂₁, and b₂₂ are q-by-q bidiagonal matrices represented implicitly by angles theta(1), ..., theta(q) and phi(1), ..., phi(q-1). b₁₁ and b₁₂ are upper bidiagonal, while b₂₁ and b₂₂ are lower bidiagonal. Every entry in each bidiagonal band is a product of a sine or cosine of theta with a sine or cosine of phi. See [Sutton09] or description of ?orcsd/?uncsd for details.

p₁, p₂, q₁, and q₂ are represented as products of elementary reflectors. See description of ?orcsd/?uncsd for details on generating p₁, p₂, q₁, and q₂ using ?orgqr and ?orglq.

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

trans

CHARACTER

= 'T':

x, u₁, u₂, v₁^t, v₂^t are stored in row-major order.

otherwise

x, u₁, u₂, v₁^t, v₂^t are stored in column-major order.

signs

CHARACTER

= 'O':

The lower-left block is made nonpositive (the "other" convention).

otherwise

The upper-right block is made nonpositive (the "default" convention).

m

INTEGER. The number of rows and columns of the matrix X.

p

INTEGER. The number of rows in x₁₁ and x₁₂. 0 ≤ p ≤ m.

q

INTEGER. The number of columns in x₁₁ and x₂₁. 0 ≤ q ≤ min(p,m-p,m-q).

x11

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (ldx11,q).

On entry, the top-left block of the orthogonal/unitary matrix to be reduced.

ldx11

INTEGER. The leading dimension of the array X₁₁. If trans = 'T', ldx11 ≥ p. Otherwise, ldx11 ≥ q.

x12

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (ldx12,m-q).

On entry, the top-right block of the orthogonal/unitary matrix to be reduced.

ldx12

INTEGER. The leading dimension of the array X₁₂. If trans = 'N', ldx12 ≥ p. Otherwise, ldx12 ≥ m-q.

x21

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (ldx21,q).

On entry, the bottom-left block of the orthogonal/unitary matrix to be reduced.

ldx21

INTEGER. The leading dimension of the array X₂₁. If trans = 'N', ldx21 ≥ m-p. Otherwise, ldx21 ≥ q.

x22

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (ldx22,m-q).

On entry, the bottom-right block of the orthogonal/unitary matrix to be reduced.

ldx22

INTEGER. The leading dimension of the array X₂₁. If trans = 'N', ldx22 ≥ m-p. Otherwise, ldx22 ≥ m-q.

work

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Workspace array, DIMENSION (lwork).

lwork

INTEGER. The size of the work array. lwork ≥ m-q

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

Output Parameters

x11

On exit, the form depends on trans:

If trans='N',

the columns of tril(x11) specify reflectors for p₁, the rows of triu(x11,1) specify reflectors for q₁

otherwise trans='T',

the rows of triu(x11) specify reflectors for p₁, the columns of tril(x11,-1) specify reflectors for q₁

x12

On exit, the form depends on trans:

If trans='N',

the columns of triu(x12) specify the first p reflectors for q₂

otherwise trans='T',

the columns of tril(x12) specify the first p reflectors for q₂

x21

On exit, the form depends on trans:

If trans='N',

the columns of tril(x21) specify the reflectors for p₂

otherwise trans='T',

the columns of triu(x21) specify the reflectors for p₂

x22

On exit, the form depends on trans:

If trans='N',

the rows of triu(x22(q+1:m-p,p+1:m-q)) specify the last m-p-q reflectors for q₂

otherwise trans='T',

the columns of tril(x22(p+1:m-q,q+1:m-p)) specify the last m-p-q reflectors for p₂

theta

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (q). The entries of bidiagonal blocks b₁₁, b₁₂, b₂₁, and b₂₂ can be computed from the angles theta and phi. See the Description section for details.

phi

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (q-1). The entries of bidiagonal blocks b₁₁, b₁₂, b₂₁, and b₂₂ can be computed from the angles theta and phi. See the Description section for details.

taup1

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (p).

Scalar factors of the elementary reflectors that define p₁.

taup2

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (m-p).

Scalar factors of the elementary reflectors that define p₂.

tauq1

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (q).

Scalar factors of the elementary reflectors that define q₁.

tauq2

REAL for sorbdb

DOUBLE PRECISION for dorbdb

COMPLEX for cunbdb

DOUBLE COMPLEX for zunbdb

Array, DIMENSION (m-q).

Scalar factors of the elementary reflectors that define q₂.

info

INTEGER.

= 0: successful exit

< 0: if info = -i, the i-th argument has an illegal value.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see Fortran 95 Interface Conventions.

Specific details for the routine ?orbdb/?unbdb interface are as follows:

x11

Holds the block of matrix X of size (p, q).

x12

Holds the block of matrix X of size (p, m-q).

x21

Holds the block of matrix X of size (m-p, q).

x22

Holds the block of matrix X of size (m-p, m-q).

theta

Holds the vector of length q.

phi

Holds the vector of length q-1.

taup1

Holds the vector of length p.

taup2

Holds the vector of length m-p.

tauq1

Holds the vector of length q.

taupq2

Holds the vector of length m-q.

trans

Must be 'N' or 'T'.

signs

Must be 'O' or 'D'.