Symmetric Eigenvalue Problems

Symmetric eigenvalue problems are posed as follows: given an n-by-n real symmetric or complex Hermitian matrix A, find the eigenvalues λ and the corresponding eigenvectors z that satisfy the equation

Az = λz (or, equivalently, zHA = λzH).

In such eigenvalue problems, all n eigenvalues are real not only for real symmetric but also for complex Hermitian matrices A, and there exists an orthonormal system of n eigenvectors. If A is a symmetric or Hermitian positive-definite matrix, all eigenvalues are positive.

To solve a symmetric eigenvalue problem with LAPACK, you usually need to reduce the matrix to tridiagonal form and then solve the eigenvalue problem with the tridiagonal matrix obtained. LAPACK includes routines for reducing the matrix to a tridiagonal form by an orthogonal (or unitary) similarity transformation A = QTQH as well as for solving tridiagonal symmetric eigenvalue problems. These routines (for FORTRAN 77 interface) are listed in Table "Computational Routines for Solving Symmetric Eigenvalue Problems". Respective routine names in Fortran 95 interface are without the first symbol (see Routine Naming Conventions).

There are different routines for symmetric eigenvalue problems, depending on whether you need all eigenvectors or only some of them or eigenvalues only, whether the matrix A is positive-definite or not, and so on.

These routines are based on three primary algorithms for computing eigenvalues and eigenvectors of symmetric problems: the divide and conquer algorithm, the QR algorithm, and bisection followed by inverse iteration. The divide and conquer algorithm is generally more efficient and is recommended for computing all eigenvalues and eigenvectors. Furthermore, to solve an eigenvalue problem using the divide and conquer algorithm, you need to call only one routine. In general, more than one routine has to be called if the QR algorithm or bisection followed by inverse iteration is used.

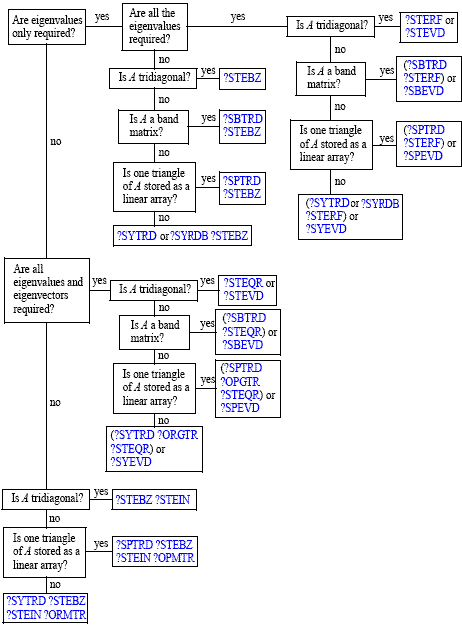
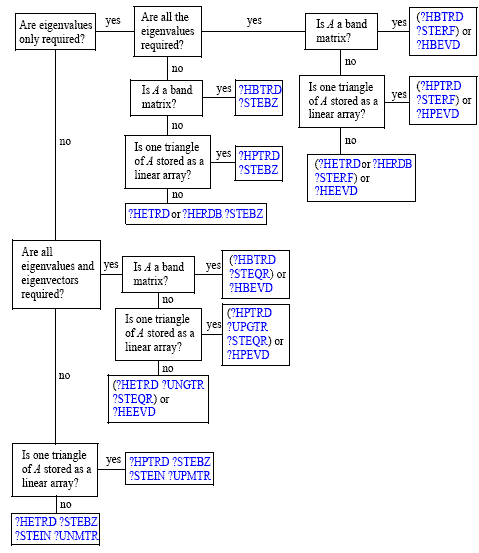
The decision tree in Figure "Decision Tree: Real Symmetric Eigenvalue Problems" will help you choose the right routine or sequence of routines for eigenvalue problems with real symmetric matrices. Figure "Decision Tree: Complex Hermitian Eigenvalue Problems" presents a similar decision tree for complex Hermitian matrices.

Decision Tree: Real Symmetric Eigenvalue Problems

?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?stevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric tridiagonal matrix using divide and conquer algorithm. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?sbtrdReduces a real symmetric band matrix to tridiagonal form. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?sbevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric band matrix using divide and conquer algorithm. ?sbtrdReduces a real symmetric band matrix to tridiagonal form. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?sptrdReduces a real symmetric matrix to tridiagonal form using packed storage. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?spevdUses divide and conquer algorithm to compute all eigenvalues and (optionally) all eigenvectors of a real symmetric matrix held in packed storage. ?sptrdReduces a real symmetric matrix to tridiagonal form using packed storage. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?sytrdReduces a real symmetric matrix to tridiagonal form. ?syrdbReduces a real symmetric matrix to tridiagonal form with Successive Bandwidth Reduction approach. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?syevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric matrix using divide and conquer algorithm. ?sytrdReduces a real symmetric matrix to tridiagonal form. ?syrdbReduces a real symmetric matrix to tridiagonal form with Successive Bandwidth Reduction approach. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?stevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric tridiagonal matrix using divide and conquer algorithm. ?sbtrdReduces a real symmetric band matrix to tridiagonal form. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?sbevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric band matrix using divide and conquer algorithm. ?sptrdReduces a real symmetric matrix to tridiagonal form using packed storage. ?opgtrGenerates the real orthogonal matrix Q determined by ?sptrd. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?spevdUses divide and conquer algorithm to compute all eigenvalues and (optionally) all eigenvectors of a real symmetric matrix held in packed storage. ?sytrdReduces a real symmetric matrix to tridiagonal form. ?orgtrGenerates the real orthogonal matrix Q determined by ?sytrd. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?syevdComputes all eigenvalues and (optionally) all eigenvectors of a real symmetric matrix using divide and conquer algorithm. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steinComputes the eigenvectors corresponding to specified eigenvalues of a real symmetric tridiagonal matrix. ?sptrdReduces a real symmetric matrix to tridiagonal form using packed storage. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steinComputes the eigenvectors corresponding to specified eigenvalues of a real symmetric tridiagonal matrix. ?opmtrMultiplies a real matrix by the real orthogonal matrix Q determined by ?sptrd. ?sytrdReduces a real symmetric matrix to tridiagonal form. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steinComputes the eigenvectors corresponding to specified eigenvalues of a real symmetric tridiagonal matrix. ?ormtrMultiplies a real matrix by the real orthogonal matrix Q determined by ?sytrd.

Decision Tree: Complex Hermitian Eigenvalue Problems

?hbtrdReduces a complex Hermitian band matrix to tridiagonal form. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?hbevdComputes all eigenvalues and (optionally) all eigenvectors of a complex Hermitian band matrix using divide and conquer algorithm. ?hbtrdReduces a complex Hermitian band matrix to tridiagonal form. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?hptrdReduces a complex Hermitian matrix to tridiagonal form using packed storage. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?hpevdUses divide and conquer algorithm to compute all eigenvalues and (optionally) all eigenvectors of a complex Hermitian matrix held in packed storage. ?hptrdReduces a complex Hermitian matrix to tridiagonal form using packed storage. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?hetrdReduces a complex Hermitian matrix to tridiagonal form. ?herdbReduces a complex Hermitian matrix to tridiagonal form with Successive Bandwidth Reduction approach. ?sterfComputes all eigenvalues of a real symmetric tridiagonal matrix using QR algorithm. ?heevdComputes all eigenvalues and (optionally) all eigenvectors of a complex Hermitian matrix using divide and conquer algorithm. ?hetrdReduces a complex Hermitian matrix to tridiagonal form. ?herdbReduces a complex Hermitian matrix to tridiagonal form with Successive Bandwidth Reduction approach. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?hbtrdReduces a complex Hermitian band matrix to tridiagonal form. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?hbevdComputes all eigenvalues and (optionally) all eigenvectors of a complex Hermitian band matrix using divide and conquer algorithm. ?hptrdReduces a complex Hermitian matrix to tridiagonal form using packed storage. ?upgtrGenerates the complex unitary matrix Q determined by ?hptrd. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?hpevdUses divide and conquer algorithm to compute all eigenvalues and (optionally) all eigenvectors of a complex Hermitian matrix held in packed storage. ?hetrdReduces a complex Hermitian matrix to tridiagonal form. ?ungtrGenerates the complex unitary matrix Q determined by ?hetrd. ?steqrComputes all eigenvalues and eigenvectors of a symmetric or Hermitian matrix reduced to tridiagonal form (QR algorithm). ?heevdComputes all eigenvalues and (optionally) all eigenvectors of a complex Hermitian matrix using divide and conquer algorithm. ?hptrdReduces a complex Hermitian matrix to tridiagonal form using packed storage. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steinComputes the eigenvectors corresponding to specified eigenvalues of a real symmetric tridiagonal matrix. ?upmtrMultiplies a complex matrix by the unitary matrix Q determined by ?hptrd. ?hetrdReduces a complex Hermitian matrix to tridiagonal form. ?stebzComputes selected eigenvalues of a real symmetric tridiagonal matrix by bisection. ?steinComputes the eigenvectors corresponding to specified eigenvalues of a real symmetric tridiagonal matrix. ?unmtrMultiplies a complex matrix by the complex unitary matrix Q determined by ?hetrd.

Computational Routines for Solving Symmetric Eigenvalue Problems

Operation

Real symmetric matrices

Complex Hermitian matrices

Reduce to tridiagonal form A = QTQH (full storage)

?sytrd  ?syrdb

?hetrd  ?herdb

Reduce to tridiagonal form A = QTQH (packed storage)

?sptrd

?hptrd

Reduce to tridiagonal form A = QTQH (band storage).

?sbtrd

?hbtrd

Generate matrix Q (full storage)

?orgtr

?ungtr

Generate matrix Q (packed storage)

?opgtr

?upgtr

Apply matrix Q (full storage)

?ormtr

?unmtr

Apply matrix Q (packed storage)

?opmtr

?upmtr

Find all eigenvalues of a tridiagonal matrix T

?sterf

 

Find all eigenvalues and eigenvectors of a tridiagonal matrix T

?steqr  ?stedc

?steqr  ?stedc

Find all eigenvalues and eigenvectors of a tridiagonal positive-definite matrix T.

?pteqr

?pteqr

Find selected eigenvalues of a tridiagonal matrix T

?stebz  ?stegr

?stegr

Find selected eigenvectors of a tridiagonal matrix T

?stein  ?stegr

?stein  ?stegr

Find selected eigenvalues and eigenvectors of f a real symmetric tridiagonal matrix T

?stemr

?stemr

Compute the reciprocal condition numbers for the eigenvectors

?disna

?disna
Parent topic: Computational Routines

Submit feedback on this help topic

Copyright © 1994 - 2011, Intel Corporation. All rights reserved.