Generates hypergeometrically distributed random values.
Syntax
Fortran:
status = virnghypergeometric( method, stream, n, r, l, s, m )
C:
status = viRngHypergeometric( method, stream, n, r, l, s, m );
Include Files
The FORTRAN 77 interfaces are specified in the mkl_vsl.f77 include file, the Fortran 90 interfaces are specified in the mkl_vsl.f90 include file, and the C interfaces are specified in the mkl_vsl_functions.h include file.
Input Parameters
Name |
Type |
Description |
|---|---|---|
method |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int |
Generation method. The specific value is as follows: See brief description of the H2PE method in Table"Values of <method> in method parameter" |
stream |
FORTRAN 77: INTEGER*4 stream(2) Fortran 90: TYPE (VSL_STREAM_STATE), INTENT(IN) C: VSLStreamStatePtr |
Fortran: Descriptor of the stream state structure. C: Pointer to the stream state structure |
n |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int |
Number of random values to be generated |
l |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int |
Lot size l |
s |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int |
Size of sampling without replacement s |
m |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(IN) C: const int |
Number of marked elements m |
Output Parameters
Name |
Type |
Description |
|---|---|---|
r |
FORTRAN 77: INTEGER Fortran 90: INTEGER, INTENT(OUT) C: int* |
Vector of n hypergeometrically distributed random values |
Description
The Hypergeometric function generates hypergeometrically distributed random values with lot size l, size of sampling s, and number of marked elements in the lot m, where l, m, s∈N∪{0}; l ≥ max(s, m).
Consider a lot of l elements comprising m "marked" and l-m "unmarked" elements. A trial sampling without replacement of exactly s elements from this lot helps to define the hypergeometric distribution, which is the probability that the group of s elements contains exactly k marked elements.
The probability distribution is given by:)
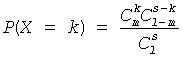
, k∈ {max(0, s + m - l), ..., min(s, m)}
The cumulative distribution function is as follows:
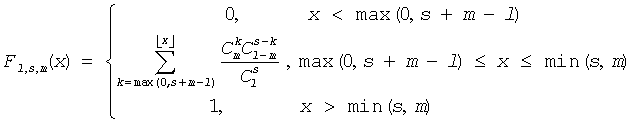
Return Values
- VSL_ERROR_OK, VSL_STATUS_OK
Indicates no error, execution is successful.
- VSL_ERROR_NULL_PTR
stream is a NULL pointer.
- VSL_RNG_ERROR_BAD_STREAM
stream is not a valid random stream.
- VSL_RNG_ERROR_BAD_UPDATE
Callback function for an abstract BRNG returns an invalid number of updated entries in a buffer, that is, < 0 or > nmax.
- VSL_RNG_ERROR_NO_NUMBERS
Callback function for an abstract BRNG returns 0 as the number of updated entries in a buffer.
- VSL_RNG_ERROR_QRNG_PERIOD_ELAPSED
Period of the generator has been exceeded.