?gebal

Syntax

FORTRAN 77:

call sgebal(job, n, a, lda, ilo, ihi, scale, info)

call dgebal(job, n, a, lda, ilo, ihi, scale, info)

call cgebal(job, n, a, lda, ilo, ihi, scale, info)

call zgebal(job, n, a, lda, ilo, ihi, scale, info)

Fortran 95:

call gebal(a [, scale] [,ilo] [,ihi] [,job] [,info])

C:

lapack_int LAPACKE_sgebal( int matrix_order, char job, lapack_int n, float* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, float* scale );

lapack_int LAPACKE_dgebal( int matrix_order, char job, lapack_int n, double* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, double* scale );

lapack_int LAPACKE_cgebal( int matrix_order, char job, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, float* scale );

lapack_int LAPACKE_zgebal( int matrix_order, char job, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, double* scale );

Include Files

The FORTRAN 77 interfaces are specified in the mkl_lapack.fi and mkl_lapack.h include files, the Fortran 95 interfaces are specified in the lapack.f90 include file, and the C interfaces are specified in the mkl_lapacke.h include file.

Description

The routine balances a matrix A by performing either or both of the following two similarity transformations:

(1) The routine first attempts to permute A to block upper triangular form:

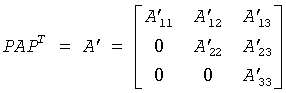
where P is a permutation matrix, and A'₁₁ and A'₃₃ are upper triangular. The diagonal elements of A'₁₁ and A'₃₃ are eigenvalues of A. The rest of the eigenvalues of A are the eigenvalues of the central diagonal block A'₂₂, in rows and columns ilo to ihi. Subsequent operations to compute the eigenvalues of A (or its Schur factorization) need only be applied to these rows and columns; this can save a significant amount of work if ilo > 1 and ihi < n.

If no suitable permutation exists (as is often the case), the routine sets ilo = 1 and ihi = n, and A'₂₂ is the whole of A.

(2) The routine applies a diagonal similarity transformation to A', to make the rows and columns of A'₂₂ as close in norm as possible:

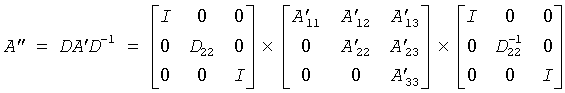
This scaling can reduce the norm of the matrix (that is, ||A'₂'₂|| < ||A'₂₂||), and hence reduce the effect of rounding errors on the accuracy of computed eigenvalues and eigenvectors.

Input Parameters

The data types are given for the Fortran interface. A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

job

CHARACTER*1. Must be 'N' or 'P' or 'S' or 'B'.

If job = 'N', then A is neither permuted nor scaled (but ilo, ihi, and scale get their values).

If job = 'P', then A is permuted but not scaled.

If job = 'S', then A is scaled but not permuted.

If job = 'B', then A is both scaled and permuted.

n

INTEGER. The order of the matrix A (n ≥ 0).

a

REAL for sgebal

DOUBLE PRECISION for dgebal

COMPLEX for cgebal

DOUBLE COMPLEX for zgebal.

Arrays:

a (lda,*) contains the matrix A.

The second dimension of a must be at least max(1, n). a is not referenced if job = 'N'.

lda

INTEGER. The leading dimension of a; at least max(1, n).

Output Parameters

a

Overwritten by the balanced matrix (a is not referenced if job = 'N').

ilo, ihi

INTEGER. The values ilo and ihi such that on exit a(i,j) is zero if i > j and 1 ≤ j < ilo or ihi < i ≤ n.

If job = 'N' or 'S', then ilo = 1 and ihi = n.

scale

REAL for single-precision flavors DOUBLE PRECISION for double-precision flavors

Array, DIMENSION at least max(1, n).

Contains details of the permutations and scaling factors.

More precisely, if p_j is the index of the row and column interchanged with row and column j, and d_j is the scaling factor used to balance row and column j, then

scale(j) = p_j for j = 1, 2,..., ilo-1, ihi+1,..., n;

scale(j) = d_j for j = ilo, ilo + 1,..., ihi.

The order in which the interchanges are made is n to ihi+1, then 1 to ilo-1.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Fortran 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see Fortran 95 Interface Conventions.

Specific details for the routine gebal interface are the following:

a

Holds the matrix A of size (n,n).

scale

Holds the vector of length n.

ilo

Default value for this argument is ilo = 1.

ihi

Default value for this argument is ihi = n.

job

Must be 'B', 'S', 'P', or 'N'. The default value is 'B'.

Application Notes

The errors are negligible, compared with those in subsequent computations.

If the matrix A is balanced by this routine, then any eigenvectors computed subsequently are eigenvectors of the matrix A'' and hence you must call ?gebak to transform them back to eigenvectors of A.

If the Schur vectors of A are required, do not call this routine with job = 'S' or 'B', because then the balancing transformation is not orthogonal (not unitary for complex flavors).

If you call this routine with job = 'P', then any Schur vectors computed subsequently are Schur vectors of the matrix A'', and you need to call ?gebak (with side = 'R') to transform them back to Schur vectors of A.

The total number of floating-point operations is proportional to n².