Nonsymmetric Eigenvalue Problems

This topic describes LAPACK routines for solving nonsymmetric eigenvalue problems, computing the Schur factorization of general matrices, as well as performing a number of related computational tasks.

A nonsymmetric eigenvalue problem is as follows: given a nonsymmetric (or non-Hermitian) matrix A, find the eigenvalues λ and the corresponding eigenvectors z that satisfy the equation

Az = λz (right eigenvectors z)

or the equation

zHA = λzH (left eigenvectors z).

Nonsymmetric eigenvalue problems have the following properties:

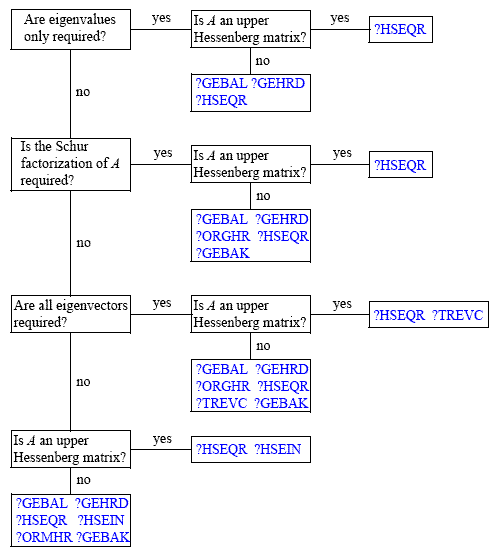
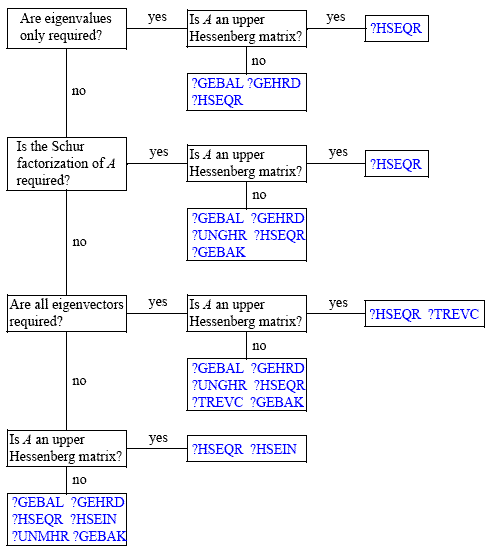
To solve a nonsymmetric eigenvalue problem with LAPACK, you usually need to reduce the matrix to the upper Hessenberg form and then solve the eigenvalue problem with the Hessenberg matrix obtained. Table "Computational Routines for Solving Nonsymmetric Eigenvalue Problems" lists LAPACK routines (FORTRAN 77 interface) to reduce the matrix to the upper Hessenberg form by an orthogonal (or unitary) similarity transformation A = QHQH as well as routines to solve eigenvalue problems with Hessenberg matrices, forming the Schur factorization of such matrices and computing the corresponding condition numbers. Respective routine names in the Fortran 95 interface are without the first symbol (see Routine Naming Conventions).

The decision tree in Figure "Decision Tree: Real Nonsymmetric Eigenvalue Problems" helps you choose the right routine or sequence of routines for an eigenvalue problem with a real nonsymmetric matrix. If you need to solve an eigenvalue problem with a complex non-Hermitian matrix, use the decision tree shown in Figure "Decision Tree: Complex Non-Hermitian Eigenvalue Problems".

Computational Routines for Solving Nonsymmetric Eigenvalue Problems

Operation performed

Routines for real matrices

Routines for complex matrices

Reduce to Hessenberg form A = QHQH

?gehrd,

?gehrd

Generate the matrix Q

?orghr

?unghr

Apply the matrix Q

?ormhr

?unmhr

Balance matrix

?gebal

?gebal

Transform eigenvectors of balanced matrix to those of the original matrix

?gebak

?gebak

Find eigenvalues and Schur factorization (QR algorithm)

?hseqr

?hseqr

Find eigenvectors from Hessenberg form (inverse iteration)

?hsein

?hsein

Find eigenvectors from Schur factorization

?trevc

?trevc

Estimate sensitivities of eigenvalues and eigenvectors

?trsna

?trsna

Reorder Schur factorization

?trexc

?trexc

Reorder Schur factorization, find the invariant subspace and estimate sensitivities

?trsen

?trsen

Solves Sylvester's equation.

?trsyl

?trsyl

Decision Tree: Real Nonsymmetric Eigenvalue Problems

?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?trevcComputes selected eigenvectors of an upper (quasi-) triangular matrix computed by ?hseqr. ?gehrdReduces a general matrix to upper Hessenberg form. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?orghrGenerates the real orthogonal matrix Q determined by ?gehrd. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix. ?gehrdReduces a general matrix to upper Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?gehrdReduces a general matrix to upper Hessenberg form. ?orghrGenerates the real orthogonal matrix Q determined by ?gehrd. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?trevcComputes selected eigenvectors of an upper (quasi-) triangular matrix computed by ?hseqr. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseinComputes selected eigenvectors of an upper Hessenberg matrix that correspond to specified eigenvalues. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?gehrdReduces a general matrix to upper Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseinComputes selected eigenvectors of an upper Hessenberg matrix that correspond to specified eigenvalues. ?ormhrMultiplies an arbitrary real matrix C by the real orthogonal matrix Q determined by ?gehrd. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix.

Decision Tree: Complex Non-Hermitian Eigenvalue Problems

?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?gehrdReduces a general matrix to upper Hessenberg form. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?gehrdReduces a general matrix to upper Hessenberg form. ?unghrGenerates the complex unitary matrix Q determined by ?gehrd. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?trevcComputes selected eigenvectors of an upper (quasi-) triangular matrix computed by ?hseqr. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?gehrdReduces a general matrix to upper Hessenberg form. ?unghrGenerates the complex unitary matrix Q determined by ?gehrd. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?trevcComputes selected eigenvectors of an upper (quasi-) triangular matrix computed by ?hseqr. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseinComputes selected eigenvectors of an upper Hessenberg matrix that correspond to specified eigenvalues. ?gebalBalances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors. ?gehrdReduces a general matrix to upper Hessenberg form. ?hseqrComputes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form. ?hseinComputes selected eigenvectors of an upper Hessenberg matrix that correspond to specified eigenvalues. ?unmhrMultiplies an arbitrary complex matrix C by the complex unitary matrix Q determined by ?gehrd. ?gebakTransforms eigenvectors of a balanced matrix to those of the original nonsymmetric matrix.

Parent topic: Computational Routines

Submit feedback on this help topic

Copyright © 1994 - 2011, Intel Corporation. All rights reserved.